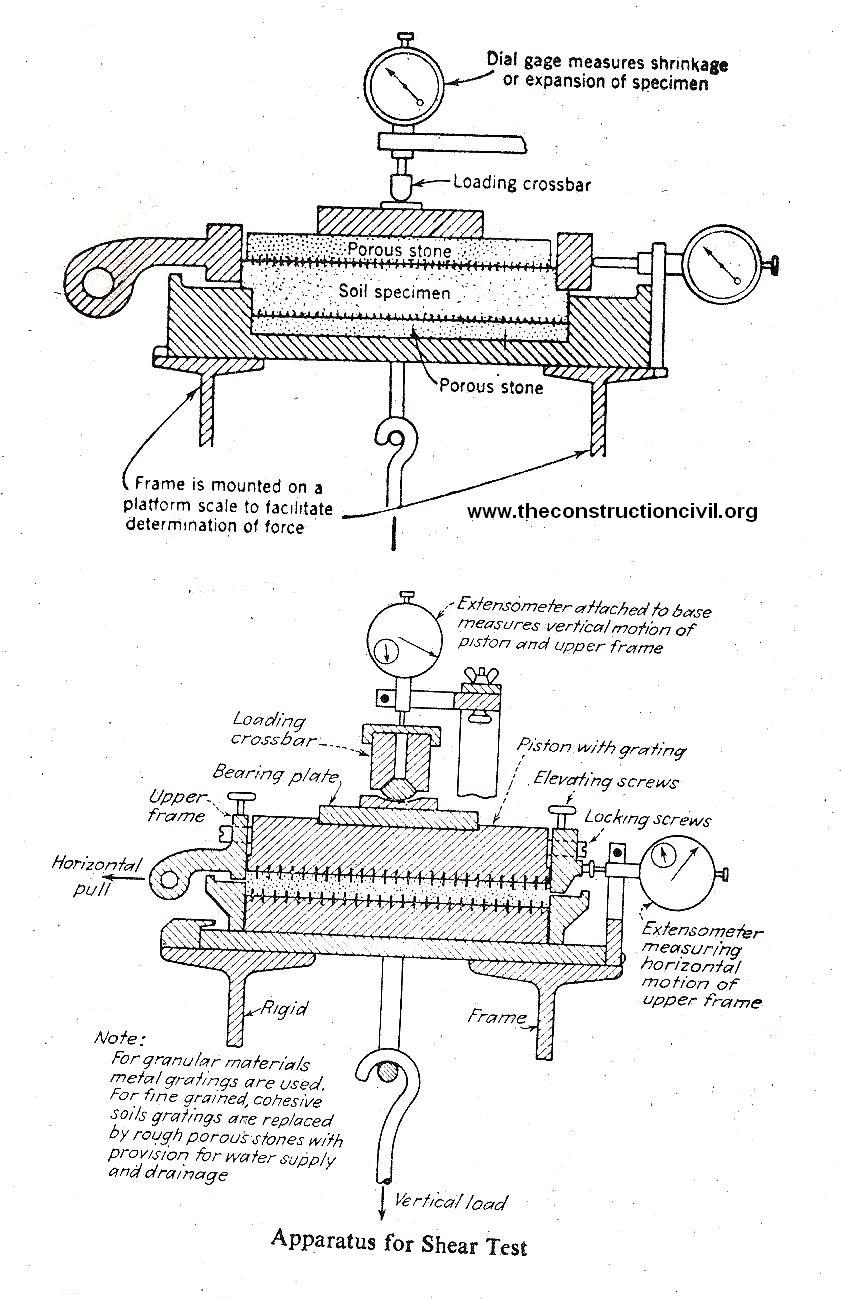
Shear Box Test of Soils – Procedure
In the shear box test, failure is caused in a pre-determined plane of the soil, the shear strength or shearing resistance and the normal stress both being measured directly, as it is a direct shear machine. The essential feature of the apparatus is a rectangular box divided horizontally into two halves, the lower half box is fixed and the upper half is movable. The soil to be tested is enclosed in the two half boxes and porous stone plates or metal plates are placed above and below the specimen. While a constant vertical compressive force is applied, a gradually increasing horizontal force is applied to the upper half of the box, thus causing the soil prism to shear along the dividing plane of the box. This measures the horizontal load required to shear a soil corresponding to any vertical normal compressive load. The test is repeated on other identical specimens under different vertical loads and the results are plotted as shearing resistance against normal vertical load (shear stress is plotted vertically and the normal stress horizontally) and straight line is drawn through the points. The equation of this line is
s=C+ n tan θ
where,
s=horizontal force divided by the area A of the cross section of the soil specimen, i.e., the unit shear resistance
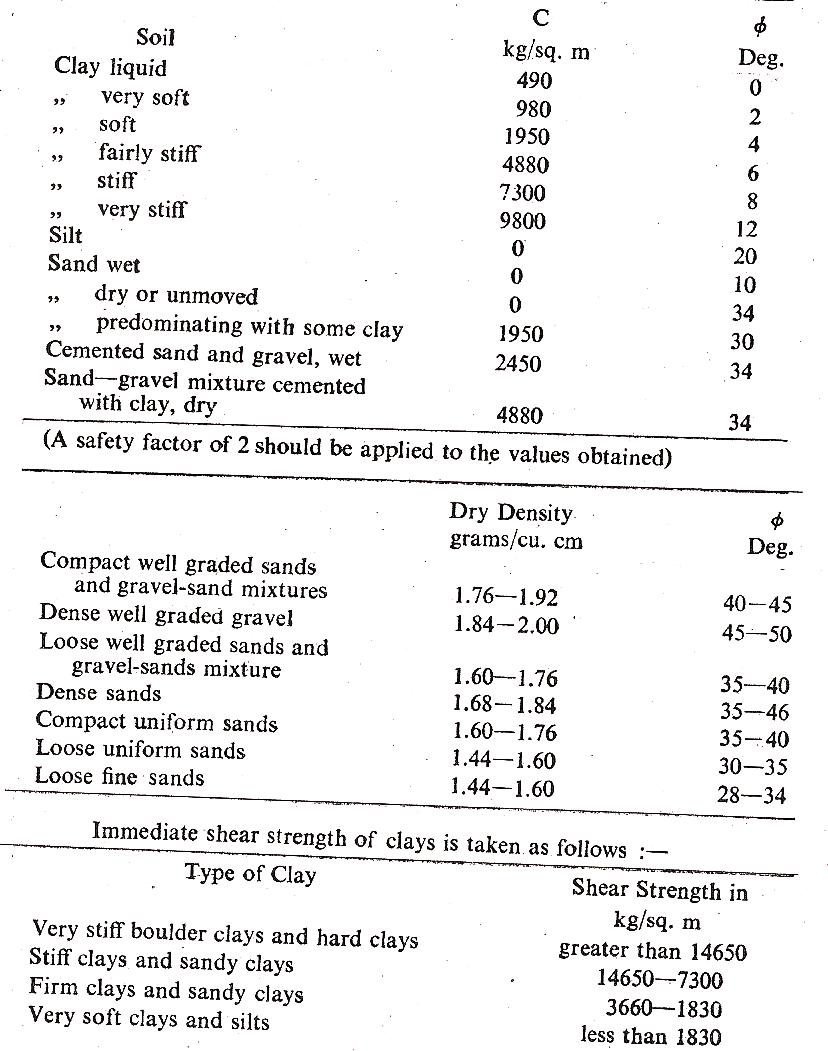
C=cohesion per unit area=the horizontal shear force under no vertical load. Cohesion for a granular soil (dry sand) is zero. Can be read off from the graph;
n=vertical normal load per unit area
θ =angle of shearing resistance or the angle of internal friction. Can be read off from the graph.
In the case of undrained saturated clays the angle of shearing resistance is zero. The true angle of internal friction of clay is seldom zero and may be as much as 26 deg.
Direct shear tests are of two kinds (1) Immediate tests, in which the horizontal load is applied as Soon as the normal vertical load begins to act, and the specimen is enclosed between metal plates. (ii) Slow tests, in which the soil is allowed to consolidate completely under each increment of vertical load. The specimens are enclosed between porous plates which allow the soil to drain.
The inter-relationship between cohesion, internal friction and stability are determined from the above equation. The unit shear resistance is composed of two parts, that furnished by the resistance of soil grains to sliding over each other and that furnished by the cohesion existing between the soil particles. By experiments the cohesion C in kg/sq. m and θ have been ascertained as given in the table below, from which the vertical load n in kg/ sq. m can be computed.
The soils subject to the higher normal stresses will ha’ lower moisture Contents and higher bulk densities than those subjected to lower normal stresses and will thus have increase in shearing resistance and cohesion with increasing normal stress.